De “Twittercrash”

Een paar dagen geleden is er iets leuks gebeurd, de moeite om eens wat dieper op in te gaan. De zogenaamde Twitter crash. Het persagentschap Associated Press kwam met een tweet dat er explosies waren in het Witte Huis en dat president Obama gewond zou zijn. We weten nu dat dat gelukkig niet echt gebeurd is. Blijkbaar was hun account gehackt en was het een vals bericht. Kort na de tweet tuimelde de beurs een serieus eindje naar beneden. Toen bekend werd dat het een nep bericht was, werd de fout onmiddellijk rechtgezet. Zie hier de Dow Jones Industrial Average index:

Vele reacties achteraf zijn in de aard van: “zo zie je maar hoe irrationeel beurzen zijn” of “gezond verstand ontbreekt meer en meer op de beurs”. Bijvoorbeeld in dit artikel in De Tijd. Dat lijken verstandige dingen om te zeggen als je ziet dat een nep Twitter bericht zo’n daling kan veroorzaken.

Ik heb daar een andere mening over. Is zo’n daling het gevolg van een gebrek aan gezond verstand? Zou kunnen, zou ook niet kunnen. Ik heb de neiging om te denken van niet. AP is een gerespecteerd persagentschap. Als zo’n persagentschap een tweet de wereld in stuurt waarin staat dat er explosies waren in het Witte Huis en dat Obama gewond is geraakt, dan gaan er als grote belegger enkele zaken door je hoofd.

Explosies in het Witte Huis? Wat is de kans dat die tweet echt is? Toch niet zo klein, want AP zijn geen knoeiers. Is dat gewoon een probleem met een of andere installatie? Een gasvuur in de keuken ofzo? Een verwarmingsketel? Heel waarschijnlijk niet, die zullen wel goed gecontroleerd worden en veiligheid staat in dat gebouw centraal. Dus dan begint men te denken, zeker met de recente bomaanslagen in het achterhoofd, dat er misschien opnieuw een wanhoopsdaad werd uitgevoerd. Granted, de kans op een terroristische aanslag in het Witte Huis is ook zeer klein. Maar eenmaal je weet dat er explosies waren is de kans op een terroristische aanslag opeens een pak groter. Dat is het verschil tussen een onconditionele kans (de kans op een terroristische aanslag in het Witte Huis) en een conditionele kans (de kans op een terroristische aanslag in het Witte huis, gegeven dat er explosies waren).

Dus je moet als belegger rekening houden met zo’n zaken. Als het geen stomme fout was van het personeel zelf, dan zou het wel eens een aanslag kunnen zijn. Wat zijn de effecten van zo’n aanslag? Wel, zo goed als zeker oorlog. Als men ontdekt welk land achter een aanslag op de president ligt, dan is het oorlog. Daar moet men dan geen enkele Amerikaan nog van overtuigen. Ondanks de grote schulden die Amerika al heeft, zal zo’n oorlog gigantisch veel geld kosten. Belastingen zouden waarschijnlijk omhoog moeten en/of men zou meer moeten lenen om dat allemaal te kunnen financieren. De kans bestaat dat zoiets de economische toestand van de U.S., die nog steeds een beetje fragiel is, terug zou schaden. En dan heb je natuurlijk de kans dat Obama niet langer president kan zijn. We weten niet hoe erg zijn verwondingen zijn. De extra systematische onzekerheid die zoiets met zich meebrengt is ook genoeg om prijzen te laten dalen. Wat is dan de impact van oorlog en politieke onzekerheid op de beurs? Een paar percent omlaag? Wie weet…

Is het dus zo irrationeel dat de DJIA opeens ongeveer een percent lager stond? Ik weet het niet. Wat is de kans dat er werkelijk een explosie was? Die valt wel mee. Wat is de kans dat de explosie een aanslag is? Als het een aanslag is, wat is de kans op oorlog en politieke onzekerheid? Vrij realistisch. En wat doet dat met de economie? Wel, het effect weten we ook niet exact. Mogelijk een negatief effect.

Al bij al is er dus veel onzekerheid. Maar is een daling van 1% dan zo’n irrationele daling? Ik denk het niet, maar ik ben niet zeker. De verwachte cashflows van beleggingen hoeven niet eens te veranderen, alleen al de grotere systematische onzekerheid bij zo’n belangrijke gebeurtenis kan de beurzen omlaag duwen. Ik zou als journalist zeker niet durven schrijven dat het gezond verstand ontbreekt op de beurzen, zoals men bij De Tijd heeft gedaan. Om dat te beoordelen moet je zeer veel extreem kleine kansen kunnen schatten om te zien of de reactie van de beurzen correct was of niet. En dat is nogal moeilijk. Niet te snel oordelen dat verstand ontbreekt op de beurs dus.

Een ander leuk aspect is dat dit voorbeeld goed laat zien hoe efficiënt die markt is. Het nieuws komt uit en de prijzen reflecteren bijna onmiddellijk de nieuwe informatie. Wanneer men dan ontdekt dat het vals was, verdwijnt die daling ook weer zeer snel. Wat mij betreft is dat perfect wat je zou verwachten in efficiënte markten. De prijzen reageren onmiddellijk op het nieuws. Maar is de markt ook rationeel in het aanpassen van haar verwachtingen? Dat kunnen we niet beoordelen. Maar als je zegt dat markten een fout hebben gemaakt, dan maak je zelf een fout. Achteraf gezien lijkt zo’n daling absurd, want de tweet was vals. Maar wij hebben nu informatie die beleggers op dat moment niet hebben. De kwaliteit van een beslissing, die beoordeel je door gebruik te maken van de informatieset die de beslissingsnemer op het moment van de beslissing ter beschiking had (lees dat gerust nog eens een tweede keer). En niet een informatieset van een paar dagen later.

Hindsight’s 20-20.

Zijn markten efficiënt? Deel 2.

(Klik hier voor deel 1)

En we gaan verder met deel 2 in onze serie over de efficiënte markthypothese en al zijn gevolgen. Ik had beloofd om het minder theoretisch te maken maar ik ben die belofte helaas niet nagekomen. Terwijl ik aan het schrijven was bleek dat er nog teveel theoretische concepten zijn die ik moet verklaren voordat we naar de praktijk kunnen. Gelukkig is theorie niet all bad. Het helpt ons om onze gedachten te structureren. Bovendien staat helemaal onderaan deze post ook nog een stukje realiteit. Laten we er dus maar aan beginnen.

De wetenschappelijke methode

Er bestaat een video van Richard Feynman die de wetenschappelijke methode uitlegt. Feynman, een heerlijke mens om naar te luisteren, legt het als volgt uit. Als wetenschappers zijn we op zoek naar wetten die ons vertellen hoe de natuur werkt. De eerste stap houdt in dat we gaan gissen wat die wet zou kunnen zijn. Dat is dus het ontwikkelen van theorie. Daarna stellen we onszelf in stap 2 de vraag: “stel dat die theorie klopt, wat zijn dan de implicaties?”. Wanneer we één of meerdere implicaties hebben gevonden, gaan we in stap 3 experimenten opzetten om te testen of de observaties die uit zo’n experiment volgen overeenstemmen met hetgeen de theorie voorspelt. Indien dat niet het geval is, is de wet fout. Heel eenvoudig: fout! Maar omgekeerd gaat dat niet op. Het is niet omdat een experiment de implicaties van een bepaalde theorie bevestigt, dat de theorie juist is. Neen, de theorie is gewoon niet fout. We kunnen nooit een theorie aanvaarden met absolute zekerheid, we kunnen ze enkel verwerpen. Ten slotte is het in stap 1 ook belangrijk om een theorie te ontwikkelen die wel degelijk weerlegd kan worden. Als je een theorie niet kunt weerleggen, is het een waardeloze theorie. Als ik een theorie ontwikkel die stelt dat we allemaal omringd worden door geesten die we op geen enkele manier kunnen waarnemen, dan is dat een waardeloze theorie, want het is onmogelijk om ze te weerleggen.

Feynman was een fysicus, geen econoom. Maar ik zie economie ook als een wetenschap, die het bovenstaande patroon moet volgen. Maar ik denk dat het verstandig zou zijn om in te zien dat economie geen exacte wetenschap is, dat het fenomenen onderzoekt waarvan het aannemelijk is dat ze veranderen doorheen de tijd. Zwaartekracht zal morgen waarschijnlijk hetzelfde concept zijn als vandaag. In de economie hebben we zelden die luxe. In ieder geval, we mogen de economische wetenschap misschien niet zo serieus nemen als bijv. de natuurkunde, maar het wetenschappelijke proces volgen blijft zeer belangrijk. Zelfs als we een hypothese keer op keer niet kunnen verwerpen en het erop lijkt dat ze opgaat in de realiteit, dan nog kunnen we nooit zeker zijn dat ze morgen nog zal gelden. In de fysica is dat ook in zekere zin, al is daar de kans veel kleiner dan een wet van vandaag morgen zal verdwijnen.

Het probleem van de gezamelijke hypotheses

De reden waarom ik spreek over dat clipje van Feyman is omdat ik het een goed vertrekpunt vind om dieper in te gaan op de efficiënte markthypothese (EMH), zie ook mijn eerste post daaromtrent. De EMH opstellen is stap 1 in het hele verhaal: gokken naar een wet. Er is echter een belangrijk probleem: de EMH is een theorie die men onmogelijk kan weerleggen. De EMH stelt dat alle beschikbare informatie in de prijs zit, maar ze zegt echter niets over welke informatie beleggers belangrijk vinden, ofwel: de informatie die in de prijs zou moeten zitten. Hoe kan je testen of alle informatie in de prijs zit als je niet weet welke informatie in de prijs zou moeten zitten? Conclusie: de EMH is een waardeloze theorie? Neen, zover zou ik niet gaan. Laten we eerst eens nadenken over een model dat ons vertelt welke informatie allemaal belangrijk is. Het lijkt logisch dat het feit dat de appeltaart van je oma lekkerder is dan de kersentaart van de lokale bakker een stukje informatie is dat niet weerspiegeld moet worden in de prijs van het aandeel van Apple. Maar welke informatie moet dan wel in zo’n prijs zitten? Om te testen of alle informatie in de prijs zit, moet je dus ook een theorie hebben die oppert welke informatie beleggers belangrijk vinden. In het jargon noemt dat een evenwichtsmodel voor risico en rendement (ik leg dit later verder uit).

Samengevat zitten we dus met twee hypothesen die we tegelijkertijd moeten testen. Om de EMH te testen, hebben we een evenwichtsmodel nodig. Telkens als we dus de EMH zouden verwerpen, zitten we met twee mogelijkheden: ofwel is is de EMH fout, ofwel is het evenwichtsmodel fout. A big problem indeed. We kunnen marktefficiëntie op zich dus nooit verwerpen. We kunnen enkel marktefficiëntie in combinatie met een evenwichtsmodel verwerpen.

Fama zelf verwoordt het in zijn paper uit 1970 als volgt:

The definitional statement that in an efficient market prices “fully reflect” available information is so general that it has no empirically testable implications. To make the model testable, the process of price formation must be specified in more detail.

Of in een latere paper:

Depending on the emphasis desired, one can say that efficiency must be tested conditional on an asset-pricing model or that asset-pricing models are tested conditional on efficiency. The point is that such tests are always joint evidence on efficiency and an asset-pricing model.

Rationaliteit, risico en het CAPM

Op zoek dus naar een evenwichtsmodel! Evenwichtsmodellen vertrekken vaak op basis van rationaliteit. Waarom? Omdat rationaliteit het makkelijker maakt om te bepalen welke informatie van belang is. Je kan makkelijk bepalen wat mensen willen als je veronderstelt dat ze rationeel zijn en dus geen rekening houden met de appeltaart van oma maar wel met het verwachte dividend van Apple. Zo’n evenwichtsmodel gebruikt dus de notie van rationele beleggers om te bepalen wat van belang is. En uiteindelijk is één zaak altijd van belang voor rationele beleggers: risico. Risico is de echte drijfveer van de financiële markten. Risico, dat is de informatie waarin beleggers geïnteresseerd zijn. De meeste beleggers (om niet te zeggen alle beleggers) zijn risico-avers. Ze houden niet van risico. Of met andere woorden: ze willen enkel risico nemen indien ze daarvoor voldoende gecompenseerd worden in de vorm van een hoger verwacht rendement. Risico bestaat in vele vele vormen, maar laten we eens kijken naar het meest bekende evenwichtsmodel: het Capital Asset Pricing Model (CAPM), ontwikkeld door William Sharpe (en ook nog onafhankelijk door anderen wiens naam ik jullie bespaar). Sharpe heeft daar trouwens een Nobelprijs voor gekregen. Het model stelt dat beleggers maar voor één soort risico compensatie vragen: marktrisico. Marktrisico is de mate waarin het rendement van een belegging mee fluctueert met het rendement van de volledige markt. In formulevorm:

In deze formule staat voor het verwachte rendement van een belegging, staat voor de risicovrije rente (de rente die je krijgt op een belegging met geen enkel risico), staat voor de mate waarin het rendement van het aandeel meeschommelt met de markt en staat voor het verwachte rendement van de marktportefeuille bovenop de risicovrije rente. We kunnen zien dat beleggers altijd een compensatie willen die minstens gelijk is aan de risicovrije rente. Dat is logisch, want het is de rente die men steeds wil krijgen, ongeacht het risico van de belegging. Waarom zou je immers beleggen in een risicovol product als je verwacht dat je daarop minder rendement zult krijgen dan op een belegging zonder risico? Daarnaast wil men ook gecompenseerd worden voor het marktrisico van een belegging, gemeten door of beta. Hoe hoger beta, hoe hoger het marktrisico en hoe hoger het verwachte rendement van de belegging. Stel een aandeel heeft een beta van 1.3. Als de markt stijgt met 1%, verwacht je dat het aandeel zal stijgen met 1.3 x 1% = 1.3%. Als de markt daalt met 5%, zou je verwachten dat het aandeel daalt met 1.3 x -5% = -6.5%. Zoals je kan zien: beta is een maatstaf voor risico. Tenslotte, wat is dan de compensatie die een belegger wil krijgen voor één eenheid beta? Wel, dat is de risicopremie: . Die premie meet wat de markt extra te bieden heeft bovenop een risicovrij product. En gegeven dit model kunnen we dus voor iedere belegging bepalen wat de relatie tussen risico en verwacht rendement is. Een evenwichtsmodel van risico en rendement, indeed. Men spreekt trouwens van evenwicht omdat het een model is dat opgaat in evenwicht, m.a.w. wanneer vraag en aanbod in evenwicht zijn.

Let’s test!

We hebben nu een voorbeeld gezien van zo’n evenwichtsmodel, het CAPM. We kunnen nu de hypothese marktefficiëntie + CAPM testen. Die plus is belangrijk, want we kunnen marktefficiëntie niet apart testen, enkel in combinatie met een evenwichtsmodel. Laten we dus veronderstellen dat markten efficiënt zijn en dat het CAPM het werkelijke model is (stap 1: het raden van een wet). Op naar stap 2! In de onderstaande grafiek toont de volle lijn aan wat de implicaties zijn van onze wet. Hoe hoger beta is, hoe hoger het rendement gemiddeld zou moeten zijn. Men tekent dus gewoon de grafische voorstelling van de formule hierboven, waarbij men en invult en 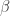laat variëren op de x-as. Nu stap 3: vergelijken met wat we observeren in de realiteit.

We nemen hiervoor alle aandelen in de U.S. en berekenen hun beta. We zouden al die aandelen nu op de grafiek kunnen plotten, maar het probleem is dat beta bijzonder onnauwkeurig geschat wordt voor individuele aandelen. We kunnen dit grotendeels oplossen door portefeuilles te vormen van aandelen. De beta’s zijn dan veel nauwkeuriger. We doen dit door de aandelen te sorteren, van lage beta naar hoge beta, en dan 10 portefeuilles te vormen met ieder evenveel aandelen erin: de 10% aandelen met laagste beta gaan samen, de volgende 10% aandelen met een iets hogere beta gaan ook samen, enzovoorts. Vervolgens berekenen we van die 10 portefeuilles het rendement en plotten we die punten op de grafiek m.b.v. zwarte vierkantjes.

Het lijkt dat de geobserveerde relatie tussen beta en rendement veel te plat is. Aandelen met lage beta krijgen een te hoge compensatie t.o.v. de CAPM voorspelling en aandelen met een hoge beta krijgen een te lage compensatie t.o.v. de CAPM voorspelling. Het ziet er dus naar uit dat de hypothese marktefficiëntie + CAPM niet de juiste is. Ze wordt verworpen door de data. Is dat omdat de prijzen niet de informatie omtrent het risico weerspiegelen (marktefficiëntie is fout), of is dat omdat beta eigenlijk geen rol speelt (CAPM is fout), dat weten we niet. Niemand kan het zeggen. Het enige wat we mogen stellen is dat ze samen niet kunnen verklaren wat we observeren.

(Er is trouwens nog een derde mogelijkheid: de methodologie deugt niet. Als je test zelf niet betrouwbaar is, dan is testen niet echt nuttig. Gelukkig blijkt na jaren en jaren onderzoek dat het daar hoogstwaarschijnlijk niet aan ligt).

Bron: Fama, E. F., & French, K. R. (2004). The Capital Asset Pricing Model: Theory and Evidence. The Journal of Economic Perspectives, 18(3), 25-46.

In realiteit lijken andere factoren het rendement van een belegging te bepalen. Beta lijkt niet zo belangrijk te zijn, andere factoren dan weer wel. Bijvoorbeeld een factor die gerelateerd is aan bedrijfsgrootte, of een factor die gerelateerd is aan value & growth. Maar dat zeer interessante verhaal hou ik voor een andere keer.

Zijn markten efficiënt? Deel 1.

Meer en meer hoor ik mensen zeggen dat markten niet efficiënt zijn. Is dat echt zo? Markten zijn zo goed als zeker niet 100% efficiënt, maar waar anderen zeggen dat markten allesbehalve efficiënt zijn, denk ik dat ze voornamelijk efficiënt zijn. Aangezien dit het topic is dat indertijd mijn interesse in de economische wetenschap echt heeft opgewekt, ga ik er enkele posts aan wijten. Ik moet benadrukken dat ik het over de financiële markten heb, niet over de reële economie. Dit is de eerste post omtrent dat topic.

Deze post zal een beetje theoretisch zijn, maar de volgende posts hieromtrent gaan veel praktischer zijn. Ik wil het hier het hebben over een zéér belangrijk stukje economische theorie die tot veel controverse leidt en die vaak ook gewoon niet correct geïnterpreteerd wordt. Mijn initiële ambitie was om alles in één post te smijten. Helaas lezen mensen (zoals ik) liever korte teksten, maar anderzijds is dit onderwerp veel te interessant om maar drie alineas over te schrijven. Dus ga ik het over meerdere posts spreiden. In deze post ga ik het puur hebben over de theorie, in latere posts ga ik het over de implicaties hebben, om het allemaal kort en luchtig te houden.

Ik ga het hebben over de efficiënte markthypothese, geformuleerd door Eugene Fama in 1970. Fama wordt door velen aanzien als de vader van de moderne finance en ik heb wel de neiging om het daarmee eens te zijn, ondanks dat ik geboren ben in een tijdperk wanneer modern finance eigenlijk al lang niet meer modern was. Fama is professor of finance aan de University of Chicago Booth School of Business. In de economische wetenschappen is de University of Chicago een bijzonder gerespecteerde universiteit, met grote namen zoals Milton Friedman, Friedrich Hayek of Robert Lucas. De “Chicago school of economics” is iedere econoom wel bekend en staat vooral voor het vrijemarkt-denken. Ik heb veel van Fama’s papers gelezen en sta telkens weer versteld van zijn creativiteit en inzicht. Dat moeten zelfs zijn intellectuele tegenstanders erkennen. Bovendien is hij een echte empirist, iemand die data gebruikt om theorieën te testen, en daar hou ik wel van. Ongetwijfeld zijn meest gekende bijdrage aan de economische wetenschap is de efficiënte markthypothese, maar was is dat eigenlijk voor een beest?

Wat is de efficiënte markthypothese?

De efficiënte markthypothese (EMH) is een eenvoudige hypothese, maar met verregaande conclusies. De EMH zegt dat prijzen op de financiële markten op ieder moment alle beschikbare informatie weerspiegelen. Een voorbeeldje. Stel dat een stuk goud vandaag 1000 dollar kost. Je weet, om een of andere reden, dat goud morgen 1050 dollar waard zal zijn. De EMH zegt dat zo’n situatie niet kan. Immers, als je weet dat goud morgen 1050 dollar waard zal zijn, dan zal je onmiddellijk goud beginnen kopen. En je zal goud blijven kopen totdat de prijs 1050 dollar is, want zolang die prijs onder de 1050 dollar blijft, maak je winst. En wanneer je geld op is zal je zelfs gaan lenen. Je koopgedrag zal de prijs opdrijven. Het resultaat is natuurlijk dat de goudprijs vandaag al 1050 dollar zal zijn, en niet 1000 dollar. Of anders gezegd: alle beschikbare informatie (jij weet dat de prijs morgen 1050 dollar zal zijn) wordt vandaag reeds weerspiegeld in de prijs (de prijs zal vandaag al 1050 dollar zijn).

Nu, dit was natuurlijk een extreem simplistisch en onrealistisch voorbeeld. Een meer realistisch voorbeeld dat je vaak kan waarnemen is wanneer bedrijven hun winst bekend maken. Je zal zien dat de aandelenprijs onmiddellijk zal reageren op die nieuwe informatie. Maar er speelt soms iets vreemds: er zijn bedrijven die hoge winsten aankondigen, maar om een of andere reden daalt toch hun aandelenprijs. Hoe kan zoiets in hemelsnaam? Het zijn toch hoge winsten? Ook nu kunnen we de EMH toepassen. Mensen die aandelen kopen houden reeds rekening met de verwachte winst wanneer ze kopen en verkopen. Dit blijft natuurlijk een onzeker getal, het is slechts een schatting. Wanneer het bedrijf dan ook daadwerkelijk met de winst naar buiten komt en het bedrag met zekerheid wordt geobserveerd, kan men de verwachte winst met de werkelijke winst vergelijken om te zien wat er met het aandeel zal gebeuren. Concreet: het is dus niet de winst op zich die telt, maar het verschil tussen de werkelijke winst en de verwachte winst. Bedrijven die onder de verwachtingen presteren, zelfs als ze winst maken, zien hun aandeel zakken. Bedrijven die het beter doen dan verwacht, zelfs als ze verlies maken, zien hun aandeel stijgen. Het is dus de verwachting die zeer belangrijk is.

De verschillende vormen van de EMH.

Er bestaan drie versies van de EMH. Er is de zwakke, de halfsterke en de sterke versie. De EMH is een hypothese. En hypothesen moet je testen, bestuderen. Je kan de hypothese formuleren dat Lady Gaga een man is, maar om het te testen zal je haar (of zijn?) broek moeten aftrekken. In 1970 waren er al veel studies die onderzocht hadden of de EMH in realiteit kon kloppen. De paper van Fama uit 1970 had tot doel om daar een mooie samenvatting van te maken. Om al die studies overzichtelijk samen te vatten heeft hij ze ingedeeld in zwakke studies, halfsterke studies en sterke studies. Dat heeft niet meteen iets met de kwaliteit van die studies te maken, maar eerder met de informatie die de studies gebruiken om tot hun conclusies te komen.

• De zwakke studies gebruiken historische informatie. Ze gingen na of het mogelijk was om toekomstig rendement te voorspellen op basis van historisch rendement. Dat is bijvoorbeeld wat Fama in zijn doctoraat heeft gedaan en waarover hij ook een mooie paper heeft geschreven in 1965. Zo berekende hij bijvoorbeeld de correlatie tussen rendement vandaag en rendement morgen (of andere tijdsintervallen) voor alle 30 Dow Jones aandelen, waaruit bleek dat die correlatie eigenlijk altijd 0 was. Met andere woorden: je kan toekomstig rendement niet voorspellen op basis van historisch rendement. Vandaag weten we hierover een pak meer, bijv. dat het soms wel mogelijk is om toekomstig rendement te voorspellen op basis van historisch rendement, maar ik ga het daarover meer hebben in de volgende posts.
• De halfsterke studies focussen zich op publieke informatie. De manier waarop dit vaak getest wordt, is door te kijken naar wat er gebeurt wanneer er nieuwe publieke informatie beschikbaar wordt (bijv. informatie over de winst, informatie over een kapitaalverhoging, etc). Zo heeft Fama, samen met Fisher, Jensen en Roll, in 1969 een studie gedaan naar stock-splits. Een stock-split is een situatie waarbij een bedrijf haar aandelen gaat opdelen. Als men bijv. een aandeel heeft dat aan 1200$ noteert, zou men ieder aandeel kunnen opsplitsen in 100 en zo dus 100 aandelen van 12$ krijgen. Dat was dan meteen ook de eerste studie ooit naar het gedrag van aandelenprijzen rond een bepaalde gebeurtenis. De studie bevestigt wat je zou verwachten op basis van de EMH: op basis van publieke informatie kan je je rendement niet opkrikken. De studie maakte trouwens gebruik van de CRSP database (the Center for Research on Security Prices, uitgesproken als “crisp”). Ze hadden die data gekozen omdat de oprichter van CRSP, Jim Lorie, bang was dat niemand de gloednieuwe CRSP data zou gebruiken en hij zijn financiering zou verliezen. Hij had een studie nodig om de data in de spotlights te plaatsen. En deze studie was dus het resultaat. De CRSP database wordt vandaag nog steeds gebruikt door een gigantische bende onderzoekers.
• De sterke studies gebruiken private informatie. Ze focussen zich dus op informatie die enkel beschikbaar is voor een kleine groep van beleggers, bijv. insiders. Fama erkent zelf dat het weinig waarschijnlijk is dat de EMH opgaat in de sterke zin, m.a.w. dat het niet zou lonen om te beleggen op basis van private informatie. Vaak zal dat wel lonen, omdat niet genoeg mensen die informatie hebben en de prijs van een belegging dus geen eerlijke compensatie is voor het risico dat je loopt. Mensen met inside information hebben naar alle waarschijnlijk dus wel degelijk een voordeel.

Zo, volgens mij heb ik nu een duidelijk, zij het vrij theoretisch, beeld geschetst van de EMH. Dat zal in de komende posts veranderen. Ik ga proberen om het een iets praktischere invulling te geven, maar nog steeds gebaseerd op wetenschap. Dan gaan we kijken naar onderzoek omtrent de hypothese en welke praktische conclusies we als beleggers daar uit kunnen trekken. Zo ga ik het bijvoorbeeld hebben over hoe een beginnende belegger best kan investeren. Moet hij zijn geld toevertrouwen aan fondsbeheerders? Ook zal ik het wat meer hebben over het voorspellen van rendement en de implicaties daarvan. De échte fun moet dus nog beginnen…